2 Часть. Математическое ожидание в покере: как выиграть с меньшими потерями. Математика в покере.

•    Бекдором называется стрит-дро или флеш-дро, при которых для составления комбинации нужно две карты. Если у Вас карманные A-K, а на флоп пришли Т-2-5. В такой ситуации для составления стрита, Вам необходимы и J, и Q.
•    Overcard Draw получается, когда Ваша карманная карта является старшей картой на флопе. Например, Ваши руки состоят из А-3. На флоп пришла комбинация  К-2-5. Для составления топ-пары, Вам необходимо, чтобы появился туз, который будет являться оверкартой. То есть в общей колоде осталось три карты, способные сделать лучше Вашу руку.
•    «Дырявый» стрит-дро («Gutshot») получается, когда Вам нужна лишь одна карта для того, чтобы сложилась комбинация. Ваши карманные карты при этом  J-T. На флоп пришли A-K-5. Для того, чтобы стрит составился, Вам необходима дама. То есть в общей колоде осталось четыре карты, способные сделать лучше Вашу руку.
•    Двусторонний стрит-дро складывается, когда Вы способны сложить стрит в паре направлений. Карты у Вас на кармане 5-6. На флоп пришли 7-8-А. Для составления стрита, Вам нужны 4 или 9. То есть в общей колоде осталось восемь карт, способные сделать лучше Вашу руку.
•    Флеш-дро складывается, когда у Вас пара карт одинаковой масти, а на флоп пришло две карты аналогичной масти. Ваши карты на кармане A♥-K♥. На флоп пришли 7♥-8♥-J♣. Для того, чтобы составить флеш, Вам необходима любая карта червовой масти. То есть в общей колоде осталось девять карт, способные сделать лучше Вашу руку.

Вам необходимо знать количество оставшихся карт в колоде (которые могут улучшить Вашу руку), для того, чтобы успешно рассчитывать матожидание для Вашей руки. Предположим, что Вашими карманными картами являются A♠-K♠, а на флопе появились две карты пиковой масти. В таком случае, мы можем сказать, что в колоде остаётся ещё девять карт пиковой масти (потому что в колоде находится по 13 карт каждой масти),  которые могут помочь Вам в составлении флеша. Но не забывайте, что это не всегда будет сильнейшая рука. Понятное дело, что любой игрок хочет составить из таких карт самую мощную руку, но, к сожалению, так получается не всегда.

Наиболее шустрые из Вас, наверняка, уже готовы задать вопрос: «Постойте! Но ведь у моего соперника среди карманных карт тоже могут быть карты пиковой масти? Это же уменьшит количество карт, которые остались в колоде? Тех карт, которые  способны улучшить мою руку?». Ответом будет и «да» и «нет». Этот фактор следует учитывать только лишь в том случае, если Вы знаете наверняка, что у Вашего оппонента на руках имеется пиковая карта. Но, обычно, Вы не можете знать, какими картами владеют Ваши оппоненты. Именно поэтому следует проводить расчёт математического ожидания, опираясь ли на те факты, которые имеете. Это как раз и есть информация о Ваших картах и количестве карт, находящихся на столе. Другими словами, Вы выполняете расчеты таким образом, будто Вы – единственный игрок за столом. А значит, в колоде осталось девять пиковых карт.

Во время подсчёта карт, которые способны улучшить Вашу руку (аутов), крайне важно быть точным в вычислениях. Далее мы рассмотрим ситуацию, в которой у Вас двусторонний стрит-дро и флеш-дро.

Вашими карманными картами являются J♦-T♦, а на столе - 8♦-Q♦-K♠. В том случае, если на стол придёт какая-либо бубновая карта, то Вы составите флеш (в колоде остаётся 9 аутов). Если вдруг придёт туз или, скажем, девятка, то Вы составите стрит (в колоде остаётся 8 аутов). Но в колоде остаются 9♦ и A♦. При вычислении аутов для флеша и стрита очень важно не ошибиться, и не посчитать дважды эти карты. Отсюда следует, что количество оставшихся карт в колоде , способных улучшить Вашу руку (9 карт + 8 карт – 2 карты) = 15 карт, а не (8 карт + 9 карт) = 17 карт, как можно было бы ошибочно подсчитать.

Бывает такое, что аут Вашу руку никаким образом не улучшает. В итоге получается, что он не является таковым. Предположим, что с двумя картами одной масти на столе, Вы желаете составить двусторонний стрит-дро. В таком случае может показаться, что Вы имеете восемь аутов для создания стрита, но при двух из данных аутов, появятся три карты одинаковой масти. Таким образом, у Ваших соперников появляются варианты для составления флеша. Так что в итоге, у Вас имеется лишь шесть аутов для того, чтобы составить стрит и получить лучшую руку.

Например, Вашими карманными картами являются J♠-8♣ (как мы видим, они разномастные), а на флопе появляются «радуга» (когда все карты разномастные) - 9♠-T♥-J♣. Для того, чтобы составить стрит, Вам необходимо, чтобы на стол пришли 7 или Q. Получается, что на каждую карту у Вас есть по 4 аута. А всего их 8. Но Вам следует обратить своё внимание ещё на один момент. Что случится, если на стол придёт Q♥? Тогда на столе будет 9♠-T♥-J♣-Q♥. А получится то, что если у кого-либо из Ваших соперников в карманных картах окажется король, то именно ему удастся составить лучший стрит (от короля). В то время как у Вас будет стрит от дамы. Вот так-то.

А вот теперь, мы можем с уверенностью констатировать, что единственная карта, действительно способная улучшить Вашу руку – это 7. То есть, эквивалент «дырявого» стрит-дро (у Вас же 4 аута). Естественно, шанс на то, что у кого-либо из Ваших соперников среди карманных карт окажется король, совсем невелик (особенно тогда, когда за столом небольшое количество игроков), но, играя на больших бетах, Вы можете попасть в не самую приятную ситуацию.

Как подсчитать матожидание для Вашей руки (немного более сложный способ).

Научившись правильно подсчитывать ауты (их количество) для Вашей руки, Вы способны вычислять % вероятности на составление комбинаций на ривере. Её достаточно просто рассчитать для отдельного конкретного случая. К примеру, для той карты, которая появится после терна на ривере. Мы просто делим наше количество аутов на количество всех карт, которые остались в колоде. Но уже для двух карт, расчёты выглядят чуть сложнее. Здесь нам необходимо исключать из наших расчётов вероятность того, что одна и та же карта может выпасть дважды. Говоря другими словами, нам нужно вычислить вероятность и отнять от неё 100 процентов. Далее мы видим пример вышеописанных вычислений:

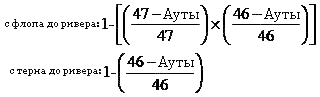
Количество карт, которые остались в колоде после флопа (из всех 52 карт вычитаем 3 на флопе и 2 Ваших карманных), обозначает цифра 47. Даже в том случае, когда в колоде останется другое количество карт, мы выполняем все расчёты таким образом, будто за столом находимся только мы. В качестве примера рассмотрим дро с двумя оверкартами, у которого для каждой из оверкарт имеется по 3 аута. То есть, для возможного составления топ-пары имеется 6 аутов.

Но, чаще всего, нам хочется видеть матожидание для нашей руки в виде пропорций. Чуть позже мы обязательно рассмотрим данный вопрос детальнее.  А сейчас, давайте взглянем на формулу, с помощью которой будем пересчитывать проценты в пропорцию:

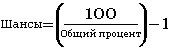
Для перевода 24 процентов в вид пропорционального математического ожидания, с которым мы будем работать, необходимо сделать так:

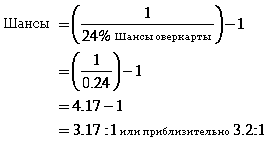
Как подсчитать матожидание для Вашей руки (способ немного проще).
Теперь Вы можете корректно высчитывать матожидание для Вашей руки в Техасском Холдеме.
Давайте рассмотрим ещё один из способов данного действия. Для понимания он должен быть немного проще.
Для того чтобы получить приблизительную вероятность (в процентах) на составление комбинации для Вашей руки после флопа, необходимо количество Ваших, уже подсчитанных аутов, умножить на 4. Для оценки процента на терне, нужно умножить число Ваших аутов на 2. Рассмотрим всё это на примере:

Примеры аутов и процентов из таблицы смотрите выше:

 
Как Вы можете сами заметить, данный метод вычисления  процентной вероятности является намного легче. Как же можно перевести проценты в пропорции? Это делается, используя ту же формулу, что и в первом способе:
 
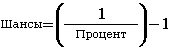
Данная формула незначительно преобразовывается и становится более простой для восприятия:

Разделив сотню на целое количество процентов, для примера на 24%, мы тут же заметим, что 100, деленное на 24, приблизительно равняется 4. Вычитая единицу, мы получаем приблизительное матожидание, равное около 3:1. Разберем подробнее данный метод на примере:

У Вас карманные карты: A♣-J♠

При флопе, состоящем из 5♣-T♦-K♦

Рассчитаем количество вероятных аутов: четыре дамы («дырявый» стрит) прибавить три туза (оверкарты) вычесть Q♦ и A♦, все это будет равняться пяти аутам.

Процентная вероятность того, что комбинация составится, равняется пяти аутам, умноженным на четыре, что составляет 20%.

Матожидание будет равняться (100 / 20) - 1= 5 – 1 = 4:1

Матожидание,  равное 4:1 означает, что  Вы имеете возможность сложить свою комбинацию единожды из каждых пяти. Если словосочетание «один раз из каждых 5» для Вас практически ничего не значит, то постарайтесь вспомнить о монетке, где матожидание того, что выпадет «орел» или «решка» равняется 1:1. У Вас выпадает «орел» в 50% бросков, следовательно, один из каждых двух вариантов выпадет «орел».

Матожидание равно Х:1, следовательно, Вы сможете сложить комбинацию в одном из (Х+1) вариантов.

Матожидание для пота.
Приобретя навык расчёта математического ожидания для Вашей руки, скорее всего, Вы начали задумываться над вопросом: «зачем мне это всё нужно?». Самый подходящий момент обсудить расчёт математического ожидания для пота. Математическим ожиданием для пота является отношением всей суммы денег в поте к цене одного колла. В случае, когда в поте находится 100 долларов, а цена одного колла составляет 10 долларов, матожидание будет равняться 5:1. Ваше матожидание для пота напрямую связано с этим отношением. И чем оно больше, тем лучше будет ваше матожидание для пота.

Матожидание для пота будет равняться Х:1, то есть, Ваша рука выиграет один раз из Х+1 случаев. И в этом случае Вы ничего не потеряете.

Вычисление математического ожидания для пота крайне важно для того, чтобы Вы понимали, какое количество раз Вам необходимо выиграть, чтобы ничего не проиграть. К примеру, если в поте находится 100 долларов, а цена одного колла равняется 10 долларам, то Вы должны понимать, что для того, чтобы ничего не проиграть, Вы должны выиграть в одном случае из одиннадцати. Попробуем объяснить данную ситуацию, что называется, на пальцах. Сыграв одиннадцать раз, Вы потратите 110 долларов. При этом выиграв один раз, Вы получите те же 110 долларов (100 долларов, которые находятся в поте + 10 долларов от Вашего колла).

Очевидной, польза вычисления математического ожидания для Вашей руки станет тогда, когда Вы сможете применять вместе и одно и второе. Как нам уже известно, шансы для Вашей руки на составление флеша (при флеш-дро) равняются 1,9:1. Предположим, что у Вас имеется рука, с потенциально сильнейшим флеш-дро. А цена колла на флопе равняется 5 долларам. Есть ли смысл коллировать? А чтобы понять это, необходимо подсчитать матожидание для пота, не так ли?
Давайте разберёмся. Допустим, что в поте имеется 15 долларов + 5 долларов (ставка Вашего соперника). Выходит, что матожидание для пота будет равняться 20:5 (4:1). Получается, что для того, чтобы не проиграть, Вам нужно выиграть хотя бы в одном случае из пяти. Но, исходя из математического ожидания для Вашего флеш-дро, Вы сможете выигрывать в каждом третьем случае! Неплохо, согласитесь.
Вам сразу должны понять, что в дальнейшем Вы получите хорошую денежную прибыль. Давайте прикинем её размер. Предположим, что данная рука будет разыграна 100 раз. Начинаться будет с флопа, а заканчиваться чеком на ривере.

Общая цена игры: 100 раздач * 5 долларов (цена за один колл) = 500 долларов
Размер пота: 15 долларов + 5 долларов (ставка) + 5 долларов (колл)
Матожидание для Вашей руки: 1,9:1 = 35% (начиная с флопа)
Общее число раздач, которые были выиграны: 100 * 35% (матожидание) = 35
Общая прибыль: общее число раздач, которые были выиграны * размер пота + общая цена игры = 35 * 25 долларов – 500 долларов = 875 долларов – 500 долларов = 375 долларов чистой прибыли.

Мы убедились, что подобный флеш-дро имеет смысл разыгрывать, так как, исходя из математического ожидания для руки и для пота, Вы в итоге получаете неплохую прибыль. Теперь сделаем небольшой, но важный вывод, запомните его:
В том случае, когда матожидание для пота выше, нежели матожидание для Вашей руки, Вы, в конце концов, получите прибыль в виде денежных знаков.

Если у Вас сложится «дырявый» стрит-дро, матожидание которого составляет всего 5:1, то, скорее всего, у вас есть необходимость коллировать, в ситуации, если матожидание для пота больше, чем 5:1. Бывает и такое, что при условии наличия у Вас хорошего дро (флеш-дро, для примера), соперник делает большой бет, и тогда матожидание Вашего пота равняется 1:1, то, разумеется, Вам нет необходимости ставить флеш, потому что в конечном счете Вы проиграете. В данной ситуации фолд или полублеф являются для Вас единственным способом, при условии, что нет оппонентов, которые смогли бы коллировать после Вас и тем самым улучшить Ваше матожидание для пота. Ваше умение помнить и считать матожидание для руки и пота сможет помочь Вам в принятии важных решений в будущем. Необходимо запомнить основное правило для прибыльности игры: матожидание для пота должно быть больше, чем для руки.

Матожидание от флопа к терну и от терна к риверу.
Имеется одно довольно важное замечание, которое нужно выделить: большинство игроков, понимающих, что называется математическим ожиданием в Техасском Холдеме, не помнят, что большая часть расчетов в теории математического ожидания от флопа к риверу предполагает, что никто не ставит бетов на терне. И потому, что на флеш-дро матожидание вероятности составления флеша равно 1,9:1, то Вы способны поставить колл в размере только 1,9:1 по отношении к поту на флопе и при условии, что соперник разрешит Вам за единоразовый колл остаться и на терне, и на ривере. К большому разочарованию, в подавляющем большинстве случаев этого не случается, по этой причине Вы должны рассчитывать матожидание для пота не для всей раздачи сразу, а для каждой попавшейся карты в отдельности.   

Для расчета математического ожидания для каждой отдельной карты пота, просто пользуйтесь математическим ожиданием, полученным от терна до ривера. Для примера, если значение математического ожидания на составление флеша от терна до ривера равняется 4:1, то матожидание на составление того же флеша от флопа до терна тоже равняется 4:1.
Для наглядности представим пример вычисления математического ожидания для пота, отражающего достаточно частый ход рассуждений:
      
Пример, когда матожидание для пота рассчитывается неверно.
Ваши руки – флеш-дро; при флопе, состоящем из 10 долларового пота и 10 долларового бета. Ваш колл при этом равняется 10 долларам (матожидание равняется 2:1).
Терн состоит из 30 долларового пота и 10 долларового бета. Ваш колл равен 10 долларам (матожидание равняется 4:1).
Результатом сотни таких раздач является суммарная стоимость игры, рассчитанная как сотня раздач, умноженная на сумму 10 долларового колла на флопе и 10 долларового колла на терне, и равняется двум тысячам долларов.
Общий результат – это разность суммы выигрыша (1750 долларов) и суммарной стоимости игры (2000 долларов), который составляет прибыль от игры (-250 долларов). Следовательно, прибыль за одну раздачу составит (-2,5 доллара).


Пример правильного расчета математического ожидания для пота.
Ваши руки – флеш-дро; при флопе, состоящем из 30 долларового пота и 10 долларового бета. Ваш колл при этом равняется 10 долларам (матожидание равняется 4:1).
Терн состоит из 50 долларового пота и 16 долларового бета. Ваш колл равен 16 долларам (матожидание равняется 4:1).
Результатом сотни таких раздач является суммарная стоимость игры, рассчитанная как сотня раздач, умноженная на сумму 10 долларового колла на флопе и 16 долларового колла на терне, и равняется двум тысячам шестистам долларам.
Суммарный выигрыш рассчитывается как произведение количества раздач (100) на вероятность выигрыша (35%) и на стоимость пота (82 доллара) и равняется 2 870 долларам.
Общий результат – это разность суммы выигрыша (2 870 долларов) и суммарной стоимости игры (2600 долларов), который составляет прибыль от игры (270 долларов). Следовательно, прибыль за одну раздачу составит 2,7 доллара.

Как показывают данные математические расчеты, ставить колл с флеш-дро при математическом ожидании для пота, равном 2:1, не стоит, при условии, что после флопа ожидаются еще и беты. Во многих случаях возможно применение понятия «возможной стоимости» (о нем разговор пойдет позже), способное помочь победить с флеш-дро и с двусторонним стрит-дро даже при условии кажущегося «нехорошего» математического ожидания. Самую большую осторожность необходимо проявлять при долгосрочном дро: оверкартах, «дырявых» стритах и сетах, которые составились при непосредственном участии Вашей карманной пары, и карт на игровом столе. Если Вы будете неправильно рассчитывать матожидание для похожих дро (то есть считать сразу от флопа до ривера), то в скором времени будете за это сильно наказаны затяжными проигрышами.  

Возможная стоимость.
Возможная стоимость – отличное понятие, которое дает возможность считать беты соперников после флопа. Если все изложенное выше описывает факт того, что Ваш соперник способен поставить бет на терне, то возможная стоимость, зачастую, используется, когда Вы думаете, что Ваш соперник колирует на ривере. Предположим, например, Вы опять обладатель флеш-дро, а матожидание для пота на терне равняется 3:1. Точно зная, что для пота матожидание не должно опускаться ниже 4:1, чтобы Ваш колл оставался выгодным, Вы принимаете решение сбросить карты. Все верно, но постойте. Тут и появляется возможная стоимость. Даже при условии, что матожидание для пота на ривере равно 3:1, Вы с высокой вероятностью способны предположить, что соперник проколлит на ривере, при условии, что Вам придет карта для составления флеша. Из этого следует, что даже при условии, что матожидание для пота на ривере равняется 3:1, если есть вероятность того, что соперник коллирует Вашу ставку на ривере, то матожидание для пота будет равняться уже 4:1, следовательно, у Вас появляется возможность коллировать на терне.  
Что касается применения возможной стоимости на практике, то это значит, что Вы способны отнимать один бет при условии расчета математического ожидания Вашего дро на терне, потому что вполне возможно, что Ваши соперники проколлируют хотя бы один бет. Если посмотреть глубже, то расчеты возможной стоимости можно использовать для розыгрыша некоторых дро, являющихся в подавляющем большинстве случаев невыгодными, но на которых есть вероятность получить довольно приличную сумму, при условии, что они сложатся. Для примера, пользуясь имиджем тайтового игрока, можно разыграть «дырявый» стрит-дро против такого же тайтового оппонента. Даже учитывая то, что это ужасная игра (надеемся, что она не окажется слишком дорогостоящей для Вас), она способна принести прибыль, при условии, что Вы знаете, что соперник попытается проверить Вас бетом или рейзом, в тот момент, когда Вы получите карту для Вашего дро. Оппонент элементарно не сможет поверить в то, что Вы разыгрываете «дырявый» стрит-дро. Из-за целого ряда причин, мы не советуем все время использовать предлагаемую стоимость и разыгрывать дро как показано на примере выше. Мы познакомили Вас с данным понятием для того, чтобы Вы сумели распознать и понять аналогичную ловушку в игре своих соперников.   

Заключение.
Способность верного расчета математического ожидания для руки и пота, является основой игры будущего покерного гения. Конечно, вероятно, что первое прочтение данной статьи, может оставить много непонятного и показаться слишком сложным. Не стоит переживать из-за этого, ведь все это проходили все известные на сегодня покерные игроки. Просто начинайте играть, пытайтесь использовать, приобретенные Вами знания. Возвращайтесь на данную страницу, при возникновении у Вас новых вопросов, связанных с расчетами математического ожидания. Потихоньку, проводя анализы уже сыгранных рук, Вы поймете, что ничего сверх естественного в данной статье не написано; нужно только лишь шаг за шагом познать эту науку, применяя полученные знания на практике.